Reacting Flows
In this area of research, we explore the possibility of solving reactive multicomponent flows in the kinetic framework of the LBM.
To that end, we formulate a system of kinetic equations for a multicomponent fluid and couple it with another system of kinetic equations for compressible hydrodynamics. The systems being coupled through pressure, momentum, composition and energy, are free of passive scalars and hence thermodynamically consistent. With a focus on practical applications, we develop boundary conditions and optimizations for efficiency and numerical stability. Apart from the LBM, we also explore the feasibility of the Particle-on-Demand (PonD) method, for compressible high Mach reactive flows.
The resulting models are useful for simulation of biological flows such as breathing; combustion in manufacturing processes, energy and transport; electrochemical flows in fuel cells; thermoacoustics etc.
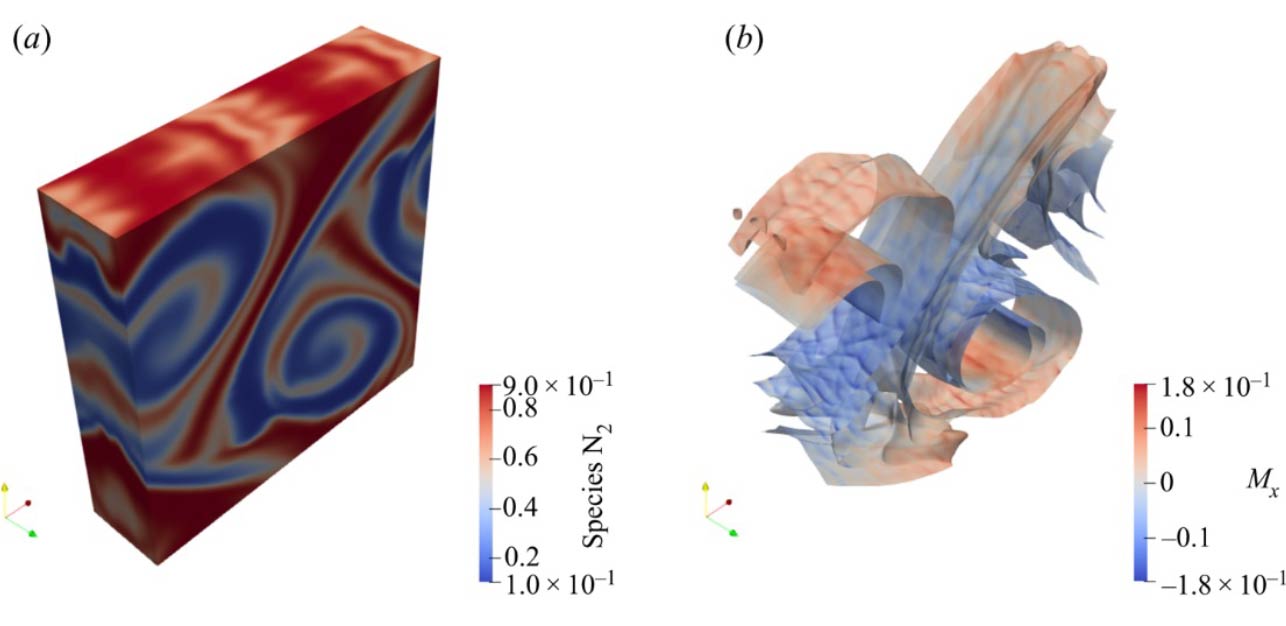
Importance of compressible mixtures is hard to overestimate because they are a prerequisite for combustion applications. However, incorporating the basic mechanism of multicomponent diffusion in gases, the Stefan–Maxwell diffusion, remains an essentially unsolved problem in the LBM context, in spite of the fact that the Stefan–Maxwell diffusion is itself a derivative of Boltzmann's kinetic theory. It is worth recalling that the Stefan–Maxwell diffusion mechanism is well recognized as a fundamental feature of gas mixtures, supported by experiment and molecular dynamics simulations. The Stefan–Maxwell model, accounts for binary interaction between each of the species pairs through pairwise diffusion coefficients and can lead to counter-intuitive effects such as uphill diffusion when a component in a ternary mixture moves from the lower to higher concentration region. We proposed a lattice Boltzmann framework for multicomponent mixtures of ideal gases with a more realistic number of coupled lattice Boltzmann equations. A new LBM system for the Stefan–Maxwell diffusion and barodiffusion comprising M lattice Boltzmann equations was proposed. Then a mean-field description of the mixture momentum and energy using the two-population setting was also presented.
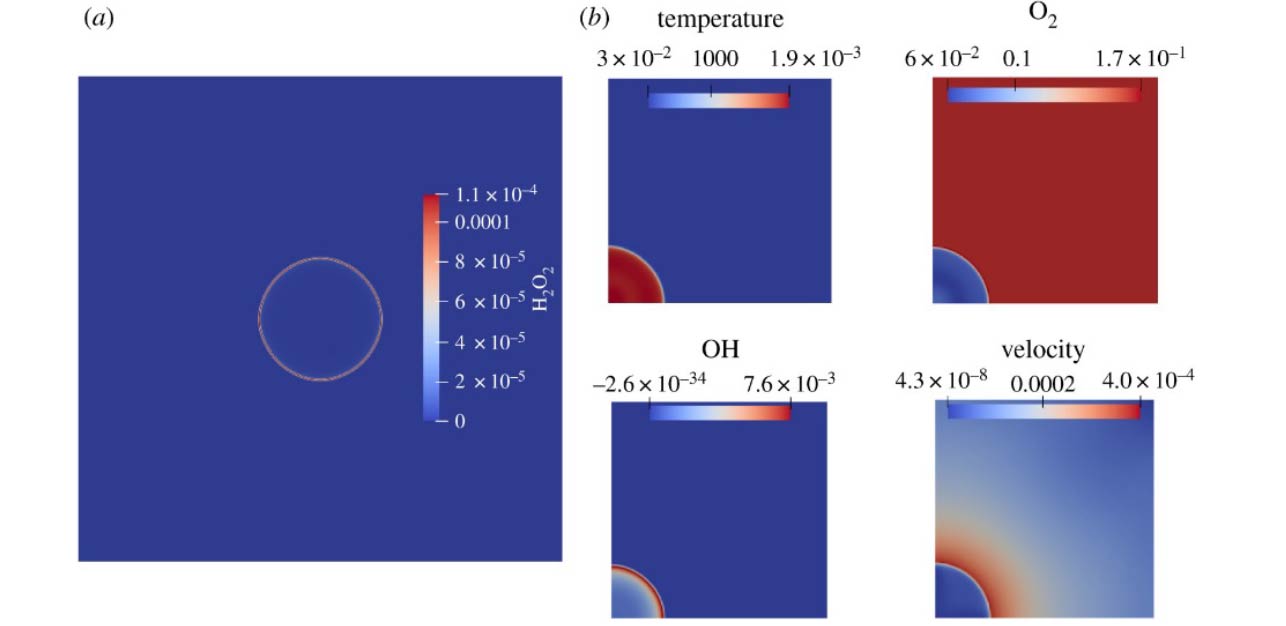
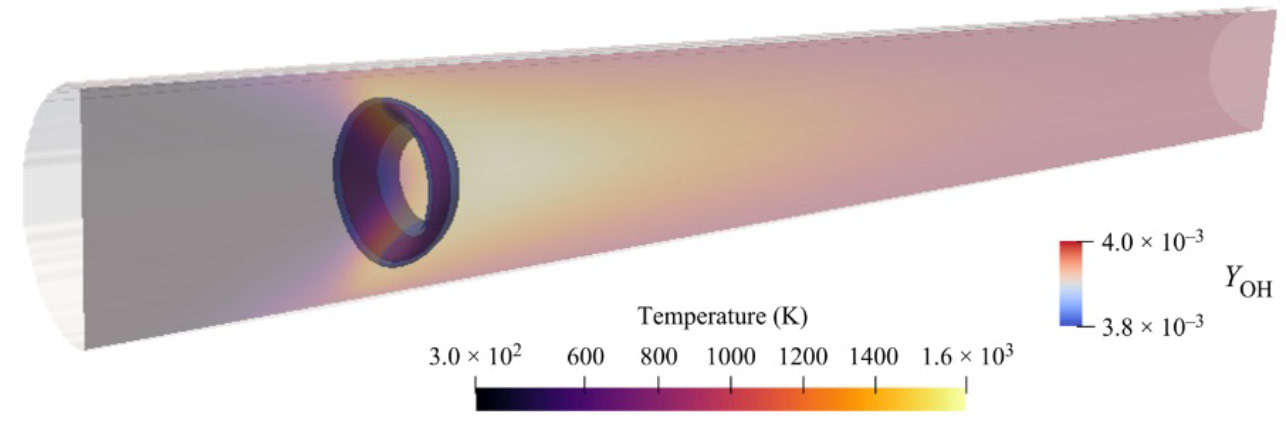
The two-population mixture LBM has also been extended to reactive flows and viability and accuracy for practical applications was shown through a variety of cases.
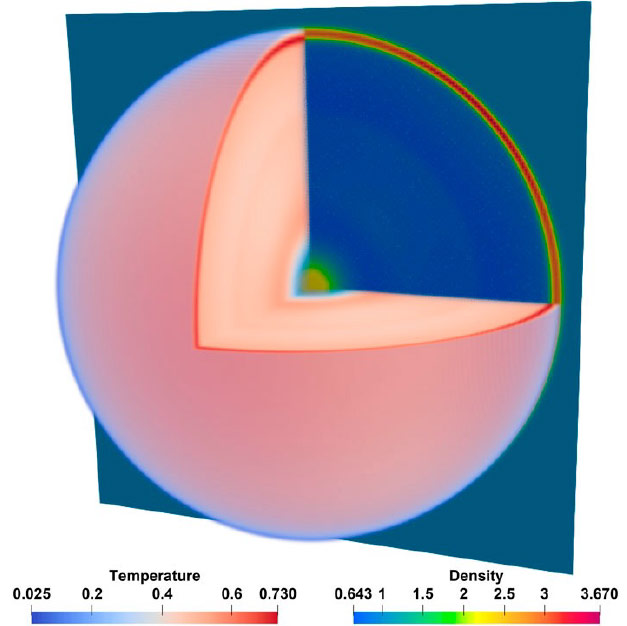
Although the progress in kinetic hydrodynamic models for detonation has been commendable, the speed of detonation waves in certain mixtures, such as hydrogen–air and acetylene–air, is in the range of 5–10 times the speed of sound. Accurate modeling of combustion with hydrogen and low carbon fuels is important from an efficiency and a safety standpoint as we move toward cleaner energy solutions for our transportation and energy needs. A potential advantage of performing detonation simulations with mesoscopic kinetic methods over the traditional macroscopic methods based on the Navier–Stokes equations is that the kinetic solvers can capture non-equilibrium hydrodynamics beyond the continuum regime.
Related Publications
Consistent lattice Boltzmann model for multicomponent mixtures
Sawant N, Dorschner B, Karlin IV.
Journal of Fluid Mechanics. 2021 Feb;909:A1.
Research Collection | external page https://doi.org/10.3929/ethz-b-000459669
Consistent lattice Boltzmann model for reactive mixtures
Sawant N, Dorschner B, Karlin IV.
Journal of Fluid Mechanics. 2022 Jun;941:A62.
Research Collection | external page https://doi.org/10.3929/ethz-b-000547521